Distansträff bestämmer jag nu till 25/26 februari. Det är en fredag och en lördag. Jag föreslår att börja klockan 9 på morgonen. Vi är nog färdiga lördag kl 15.
Vi ska göra sådana laborationer som kräver lite mer avancerad apparatur än en slinky, men vi har också en samling små experiment som jag ska demonstrera.
Tillägg: Eftersom tåget kommer 8:55, får vi nog tillägga en akademisk kvart - vi börjar alltså kl. 9:15.
Ett tillägg till: Vi håller till i sal D0069 och D0070. Det är alltså fysikavdelningens lokaler i källaren i hus D. Ingången till hus B/D är inte så svårt att hitta, men för dem som har en smart mobil finns det en app som visar vägen på Linnéuniversitetet.
tisdag 25 januari 2011
söndag 23 januari 2011
Hemlab - slinky
Vi gjorde den här laborationen efter lektionen i torsdags. Det gav resultat som stämde rätt så bra överens med varandra. Som hemlaboration är det lite svårare. Särskilt är det svårare att bestämma spänningen. På campus använde vi dynamometrar. Ni som är lärare kan nog låna en på er skola. Eller man kan improvisare något med en trissa och en tyngd så att man drar ut slinkyn till en känd spännkraft.
Ni kan hjälpa varandra med fiffiga lösningar här nere, samt redovisa era resultat. Och ja, detta är obligaroriskt.
Ni kan hjälpa varandra med fiffiga lösningar här nere, samt redovisa era resultat. Och ja, detta är obligaroriskt.
Transversella vågor på en sträng - en liten dimensionsanalys
För att få transversella vågor på ett snöre, måste det finnas en kraft som driver en utbuktning tillbaka till en rät linje. Det är snörets dragspänning, en kraft i linans längdriktning. Om strängen inte är rak, ger denna kraft också en komponent vinkelrät på strängen, se till exempel figur 16.7 i Benson.
Det är rimligt att anta att våghastigheten ökar med spänningen T i snöret. Det är också rimligt att den är långsammare ju större massa (tröghet) en sträng har. Och det viktiga är inte strängens totala massa (som ju är större för en lång sträng), utan dess massa per långdenhet (linjär densitet rho ϱ).
Nu tar vi en liten genväg och antar att våghastigheten beror på förhållandet T/ϱ. Vilka enheter har nu detta förhållande? Dragspänning är kraft som uttrycks i newton, och om man kommer ihåg att F=ma ser man att det har grundenheter kg·m/s². Man ser att förhållandet T/ϱ har enheter m²/s². Och då kan man dra slutsatsen att våghastigheten för transversella vågor är proportionell mot √T/ϱ.
Detta är det enda sättet att kombinera dragspänning och linjär densitet för att få något med enhet (dimension) av hastighet. Den här typen av betraktelse kan inte ge numeriska faktorer (som till exempel en faktor 2π), men den är ganske kraftfull i alla fall, även på tentor.
Och i det här fallet är den numeriska faktor lika med ett:

Det är rimligt att anta att våghastigheten ökar med spänningen T i snöret. Det är också rimligt att den är långsammare ju större massa (tröghet) en sträng har. Och det viktiga är inte strängens totala massa (som ju är större för en lång sträng), utan dess massa per långdenhet (linjär densitet rho ϱ).
Nu tar vi en liten genväg och antar att våghastigheten beror på förhållandet T/ϱ. Vilka enheter har nu detta förhållande? Dragspänning är kraft som uttrycks i newton, och om man kommer ihåg att F=ma ser man att det har grundenheter kg·m/s². Man ser att förhållandet T/ϱ har enheter m²/s². Och då kan man dra slutsatsen att våghastigheten för transversella vågor är proportionell mot √T/ϱ.
Detta är det enda sättet att kombinera dragspänning och linjär densitet för att få något med enhet (dimension) av hastighet. Den här typen av betraktelse kan inte ge numeriska faktorer (som till exempel en faktor 2π), men den är ganske kraftfull i alla fall, även på tentor.
Och i det här fallet är den numeriska faktor lika med ett:

fredag 21 januari 2011
Reflektion och stående vågor
I högra delen av Hewitts figur 19.13 om stående vågor förklaras dessa som en summa av två fortskridande vågor: en infallande våg som går till höger och en reflekterad våg som går till vänster, se även denna interaktiva version.
Här är det viktigt för förståelsen att man ser att reflektionen mot fast ände är inverterad (filmsnutt). Och att en fri ände reflekterer utan inversion. Det har jag visat i föreläsningssalen med en puls på den tunga långsamma fjädern som låg på golvet. Jag visade ochså följande animeringar, där jag hade konstruerat en "spegelvåg" på andra sidan, som korsar den infallande vågen vid strängens ände:

Figuren kan se lite förvirrande ut när båda fortskridande vågorna är i fas och förstärker varandra. I en stillastående ritning ser de ju inte alls ut att vara inverterade. Men i följande rörliga bild är det tydligt att den reflekterade vågen är inverterad på pulsens framsida:

Matematiskt kan en enkelt harmonisk stående våg skrivas som en summa av två fortskridande vågor: en sinusvåg som går åt ena hållet och en likadan sinusvåg som går åt andra hållet.
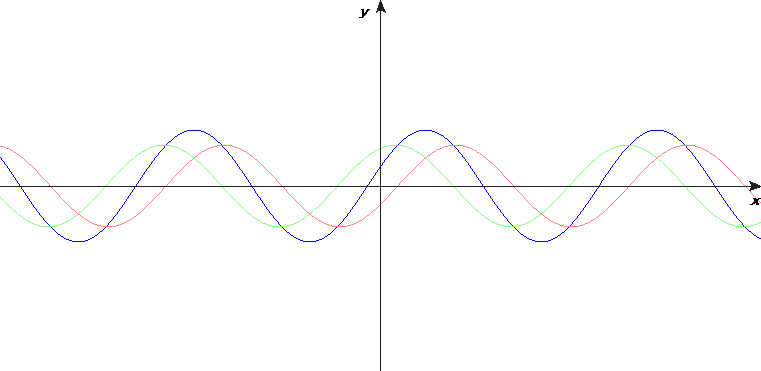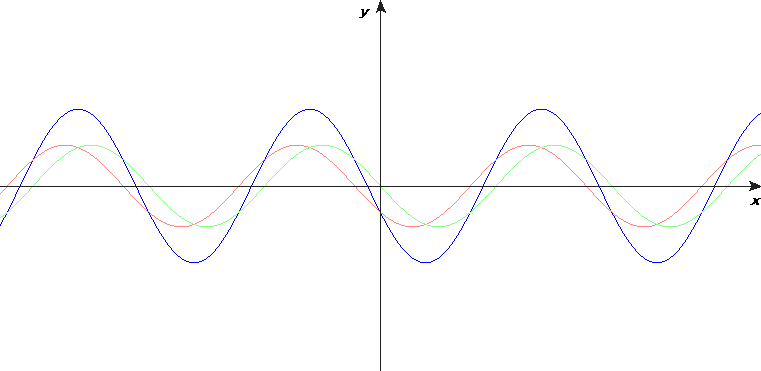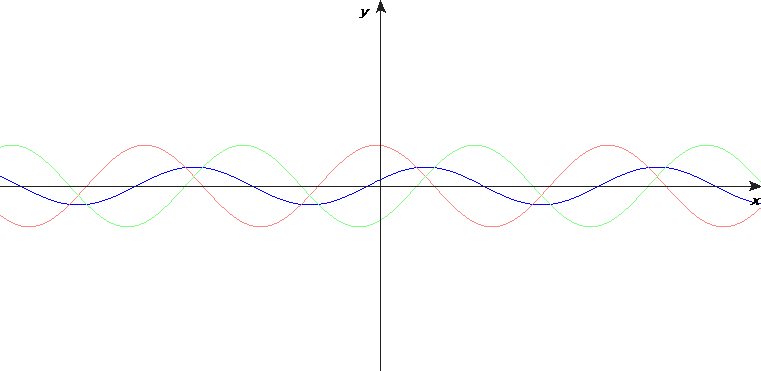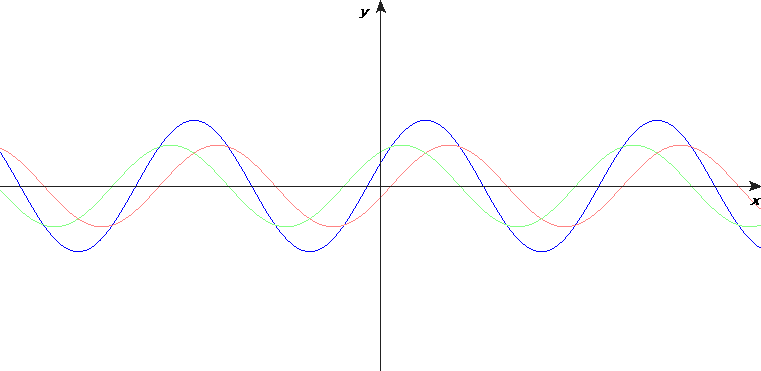
Här är det viktigt för förståelsen att man ser att reflektionen mot fast ände är inverterad (filmsnutt). Och att en fri ände reflekterer utan inversion. Det har jag visat i föreläsningssalen med en puls på den tunga långsamma fjädern som låg på golvet. Jag visade ochså följande animeringar, där jag hade konstruerat en "spegelvåg" på andra sidan, som korsar den infallande vågen vid strängens ände:

Figuren kan se lite förvirrande ut när båda fortskridande vågorna är i fas och förstärker varandra. I en stillastående ritning ser de ju inte alls ut att vara inverterade. Men i följande rörliga bild är det tydligt att den reflekterade vågen är inverterad på pulsens framsida:

Matematiskt kan en enkelt harmonisk stående våg skrivas som en summa av två fortskridande vågor: en sinusvåg som går åt ena hållet och en likadan sinusvåg som går åt andra hållet.

måndag 17 januari 2011
Introduktionsmöte
... för kursen 1FY803 Vågrörleselära & Optik ska vara nu på eftermiddagen. Det här är platsen för mer eller mindre koherenta anteckningar i marginalen från min sida. Ni är välkomna att använda bloggens kommentarfält, också för kommunikation med varandra.
Det ska bli spännande att de hur många deltagare det blir i år. Jag räknar ihop till 44 anmälda på en massa olika listor. Ni kan försöka registrera er här. Om det inte går, meddela mig, och jag ska kryssa in er på registreringslistorna.
Tyvärr, tyvärr glömde jag sätta igång inspelningen under föreläsningens första timme. Den andra timman kan man se här.
Det ska bli spännande att de hur många deltagare det blir i år. Jag räknar ihop till 44 anmälda på en massa olika listor. Ni kan försöka registrera er här. Om det inte går, meddela mig, och jag ska kryssa in er på registreringslistorna.
Tyvärr, tyvärr glömde jag sätta igång inspelningen under föreläsningens första timme. Den andra timman kan man se här.
Prenumerera på:
Kommentarer (Atom)